Introdução ao Sistema Numérico Decimal
O sistema numérico decimal é o sistema de numeração mais amplamente utilizado em todo o mundo. Ele utiliza 10 algarismos diferentes, de \(0\) a \(9\), para representar todos os números. Cada posição em um número tem um valor específico com base na potência de 10. Desse modo, dizemos que ele é posicional.
Algarismos Decimais
Os algarismos decimais são simplesmente os números de \(0\) a \(9\). Quando combinados em diferentes ordens, esses algarismos formam todos os números possíveis no sistema decimal. Cada algarismo possui um grau de importância que depende da sua posição, regido por uma potência de 10, também chamado de ordem.
Posições e Valor Posicional
A posição de um algarismo em um número é crucial. Vamos ver como funciona com um exemplo: \(2846\)
- O algarismo 6 está na posição das unidades, representando \(6 \cdot 10^0\);
- O algarismo 4 está na posição das dezenas, representando \(4 \cdot 10^1\);
- O algarismo 8 está na posição das centenas, representando \(8 \cdot 10^2\);
- O algarismo 2 está na posição dos milhares, representando \(2 \cdot 10^3\).
O valor total do número é a soma desses valores posicionais:
\(2846 = \) \(6 \cdot 10^0 + 4 \cdot 10^1 + 8 \cdot 10^2 + 2 \cdot 10^3\).
Classes Numéricas
No sistema de numeração decimal, cada algarismo desempenha um papel crucial em uma posição específica, formando ordens que, por sua vez, são agrupadas em classes. As três principais classes são: das unidades simples, dos milhares e dos milhões.
| Casa dos Milhões | Casa dos Milhares | Casa das Unidades Simples | ||||||
|---|---|---|---|---|---|---|---|---|
| C. de Milhão | D. de Milhão | U. de Milhão | C. de Milhar | D. de Milhar | U. de Milhar | Centenas | Dezenas | Unidades |
A leitura das ordens ocorre da direita para a esquerda, sendo a 1ª ordem a das unidades, a 2ª ordem a das dezenas, a 3ª ordem a das centenas, e assim por diante.
Explorando Classes e Ordens com Exemplos Numéricos
Exemplo 1: Decomponha o número 3.214 e indique o significado de cada algarismo em relação à ordem.
| Ordem | Algarismo | Valor Posicional |
|---|---|---|
| 3 | 3 | Três unidades de milhar |
| 2 | 2 | Duas centenas |
| 1 | 1 | Uma dezena |
| 0 | 4 | Quatro unidades |
A decomposição pode ser feita dessa forma:
\(3.214\) \(= 3 \cdot 10^3 + 2 \cdot 10^2 + 1 \cdot 10^1 + 4 \cdot 10^0\).
Assim, a escrita por extenso do número \(3.214\) é "três mil duzentos e quatorze".
Exemplo 2: Decomponha o número 8.765.432 e indique o significado de cada algarismo em relação à ordem.
| Ordem | Algarismo | Valor Posicional |
|---|---|---|
| 6 | 8 | Oito unidades de milhão |
| 5 | 7 | Sete centenas de milhar |
| 4 | 6 | Seis dezenas de milhar |
| 3 | 5 | Cinco unidades de milhar |
| 2 | 4 | Quatro centenas |
| 1 | 3 | Três dezenas |
| 0 | 2 | Duas unidades |
Decompondo se torna:
\( 8.765.432\) = \(8 \cdot 10^6 + 7 \cdot 10^5 + 6 \cdot 10^4 + 5 \cdot 10^3\) \( + 4 \cdot 10^2 + 3 \cdot 10^1 + 2 \cdot 10^0 \).
Assim, a escrita por extenso do número \( 8.765.432 \) é: "oito milhões setecentos e sessenta e cinco mil quatrocentos e trinta e dois".
Observação: Além das classes apresentadas, existem as classes dos bilhões, trilhões etc., cada uma com três ordens. Nos exemplos, utilizamos apenas números naturais, mas é possível estender o raciocínio do valor posicional de cada algarismo para a parte decimal de um número real.
Exemplo Adicional: O número 6.789,12 é formado por 6 números, sendo: 6 milhares, 7 centenas, 8 dezenas, 9 unidades, 1 décimo e 2 centésimos.
Observe que para números com casa decimal, a ordem decimal passa a ser a partir da vírgula e da esquerda para a direita.
Prática
(Enem 2022) Ao escutar a notícia de que um filme recém-lançado arrecadou, no primeiro mês de lançamento, R$ 1,35 bilhão em bilheteria, um estudante escreveu corretamente o número que representa essa quantia, com todos os seus algarismos.
O número escrito pelo estudante foi:
A. 135 000,00.
B. 1 350 000,00.
C. 13 500 000,00.
D. 135 000 000,00.
E. 1 350 000 000,00.
(Enem 2016) Ábaco é um antigo instrumento de cálculo que usa notação posicional de base dez para representar números naturais. Ele pode ser apresentado em vários modelos; um deles é formado por hastes apoiadas em uma base. Cada haste corresponde a uma posição no sistema decimal e nelas são colocadas argolas; a quantidade de argolas na haste representa o algarismo daquela posição. Em geral, colocam-se adesivos abaixo das hastes com os símbolos U, D, C, M, DM e CM que correspondem, respectivamente, a unidades, dezenas, centenas, unidades de milhar, dezenas de milhar e centenas de milhar, sempre começando com a unidade na haste da direita e as demais ordens do número no sistema decimal nas hastes subsequentes (da direita para esquerda), até a haste que se encontra mais à esquerda. Entretanto, no ábaco da figura, os adesivos não seguiram a disposição usual.
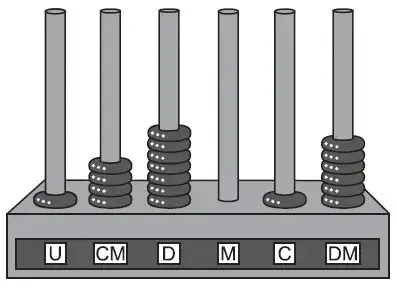
Nessa disposição, o número que está representado na figura é:
A. 46 171.
B. 147 016
C. 171 064.
D. 460 171.
E. 610 741.
Resolução 1
Observe que o algarismo 1 da extremidade à esquerda indica uma unidade de bilhão (um bilhão). Assim, o algarismo 3 indica três centenas de milhão (trezentos milhões), e o
algarismo 5 indica cinco dezenas de milhão (cinquenta milhões). Completamos as demais ordens com zeros para formar a escrita completa do número:
1 350 000 000
Por fim, como o número representa um valor monetário, acrescentamos dois zeros após a vírgula para os centavos.
1 350 000 000,00
| Casa dos Bilhões | Casa dos Milhões | Casa dos Milhares | Casa das Unidades Simples | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 3 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Alternativa E.
Outra Forma de Explicação
Vamos analisar o número 1.350.000.000 de outra forma. Cada grupo de três algarismos em um número é chamado de ordem. Começando da direita para a esquerda, temos as ordens:
Então, ao ler o número, o algarismo 1 está na ordem da Casa dos Milhões, indicando um bilhão. O algarismo 3 está na ordem da Casa dos Milhões, indicando trezentos milhões, e o algarismo 5 está na ordem da Casa dos Milhões, indicando cinquenta milhões.
Completamos as demais ordens com zeros. No final, temos 1 bilhão, 350 milhões. Para representar um valor monetário, acrescentamos dois zeros após a vírgula para os centavos:
1 350 000 000,00
Portanto, a resposta é equivalente a "Um bilhão, trezentos e cinquenta milhões e zero centavos".
Resolução 2
Organizando as hastes na disposição usual:
Observe que as classes estão misturadas. Dito isso, é necessário organizá-las. As classes citadas na questão são, em ordem: Centenas de Milhar, Dezenas de milhar, Milhar, Centenas, Dezenas e Unidade.
Respectivamente, os números que acompanham esas classes na tabela, são: 4, 6, 0, 1, 7 e 1. Assim, o número formado é: 460171.
O que leva à alternativa D.