Conjuntos Numéricos

O estudo dos conjuntos numéricos emerge da noção de contagem, que é uma relação direta e unívoca entre dois ou mais elementos, e da realização de operações entre os números do conjunto. A partir dessa base, adentramos em um vasto mundo de números que compõem os conjuntos numéricos, cada um com suas características distintas e propriedades únicas.

Números Naturais

Números Naturais (N): O conjunto dos números naturais é definido como:
\( \mathbb{N} = \{0, 1, 2, 3, 4, 5, \ldots\} \)
onde \( 0 \) é o primeiro número natural e cada número natural sucessivo é obtido adicionando-se 1 ao número anterior. Os números naturais são utilizados para contar e representar quantidades inteiras não negativas, como o número de objetos em uma coleção, a contagem de anos, entre outros. É bastante comum pensar nos Naturais como sendo todos os infinitos números positivos.

Também é interessante pensar na reta numérica para construir a noção de como os conjuntos são organizados nela. Observe que uma das características dos naturais é que um número sucessor de outros há uma distância padrão entre eles que na imagem abaixo foi representada por "u". Você pode substituir o "u" por 1 e os números naturais serão formados.

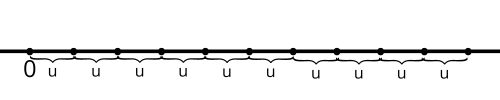
Propriedades dos Números Naturais

Infinitude: O conjunto dos números naturais é infinito, o que significa que não há um maior número natural. Você sempre pode adicionar 1 a qualquer número natural para obter outro número natural maior.
Ordenação: Os números naturais estão ordenados de forma crescente. Isso significa que cada número natural é maior que os anteriores. Por exemplo, 1 é menor que 2, que é menor que 3, e assim por diante.
Propriedade de fechamento sob adição: A adição de dois números naturais sempre resulta em outro número natural. Por exemplo, se você somar dois números naturais, como 2 e 3, o resultado será outro número natural, neste caso, 5.
Propriedade de fechamento sob multiplicação: A multiplicação de dois números naturais sempre resulta em outro número natural. Por exemplo, se você multiplicar dois números naturais, como 2 e 3, o resultado será outro número natural, neste caso, 6.
Propriedade de multiplicação com 1: Qualquer número natural multiplicado por 1 resulta no próprio número natural. Por exemplo, \(1 \times n = n\), onde \(n\) é qualquer número natural.
Propriedade de não-existência de inverso aditivo: Os números naturais não têm inversos aditivos. Isso significa que não há um número natural que, quando adicionado a outro número natural, resulte em 0.
Propriedade de não-existência de inverso multiplicativo: Com exceção do número 1, os números naturais não têm inversos multiplicativos. Isso significa que não há um número natural que, quando multiplicado por outro número natural, resulte em 1.

Observe que não há um fechamento nos naturais sobre as operações de subtração e divisão. Por exemplo: a operação 3 + 2 com certeza é Natural, mas a operação 2 - 3 não resulta em um número natural. Para resolver esse problema foi criado o conjunto dos Números Inteiros.

Números Inteiros

Números Inteiros (\( \mathbb{Z}\)): Os números inteiros consistem em todos os números naturais (incluindo o zero) e seus respectivos negativos, também chamados de opostos, bem como o zero. Formalmente, o conjunto de números inteiros é representado por \( \mathbb{Z}\) e é definido como:

\( \mathbb{Z} = \{...-5,-4 ,-3 ,-2 , -1, 0, 1, 2, 3, 4, 5 \ldots\} \)

Os números inteiros incluem números positivos, negativos e o zero. Eles são usados para representar quantidades completas, incluindo ganhos e perdas, débitos e créditos, entre outros.

Fazendo a expansão da reta numérica, os números inteiros agora passam a ocupar posições a esquerda do "0" onde esses números serão os com sinal negativo (-). É importate notar que no conjuntos dos Naturais não é necessário o uso de sinal determinante, mas nos Inteiros, sim, para poder identificar em qual sentido o número se localiza.

Subconjuntos dos Números Inteiros

Números Naturais (\( \mathbb{N}\)): Este conjunto inclui todos os números inteiros positivos, começando de 1 e indo até o infinito. Formalmente, é representado por \( \mathbb{N}\) e é definido como: \( \mathbb{N} = \{1, 2, 3, \ldots\} \)
Números Inteiros Positivos (\( \mathbb{Z}^+\)): Este subconjunto inclui todos os números inteiros positivos, incluindo o zero. Formalmente, é representado por \( \mathbb{Z}^+\) e é definido como: \( \mathbb{Z}^+ = \{0, 1, 2, 3, \ldots\} \)
Números Inteiros Negativos (\( \mathbb{Z}^-\)): Este subconjunto inclui todos os números inteiros negativos, incluindo o zero. Formalmente, é representado por \( \mathbb{Z}^-\) e é definido como: \( \mathbb{Z}^- = \{\ldots, -3, -2, -1, 0\} \)
Números Inteiros Positivos Não Nulos (\(\mathbb{Z}_*^+\)): Este subconjunto inclui todos os números inteiros positivos, excluindo o zero. Formalmente, é representado por \(\mathbb{Z}_*^+\) e é definido como: \( \mathbb{Z}_*^+ = \{ +1, +2, +3, \ldots\}\)
Números Inteiros Negativos Não Nulos (\(\mathbb{Z}_*^-\)): Este subconjunto inclui todos os números inteiros negativos, excluindo o zero. Formalmente, é representado por \(\mathbb{Z}_*^-\) e é definido como: \( \mathbb{Z}_*^- = \{\ldots, -3, -2, -1\} \)

Propriedades dos Números Inteiros

Infinitude: O conjunto dos números inteiros é infinito, o que significa que não há um maior número inteiro. Você sempre pode adicionar 1 a qualquer número inteiro positivo para obter outro número inteiro maior. Da mesma forma, pode-se subtrair 1 de qualquer número inteiro negativo para obter outro número inteiro menor.
Ordenação: Os números inteiros estão ordenados de forma crescente e decrescente. Isso significa que cada número inteiro positivo é maior que os anteriores, e cada número inteiro negativo é menor que os anteriores. Por exemplo, -3 é menor que -2, que é menor que -1, e assim por diante, enquanto 1 é menor que 2, que é menor que 3, e assim por diante.
Propriedade de fechamento sob adição: A adição de dois números inteiros sempre resulta em outro número inteiro. Por exemplo, se você somar dois números inteiros, como 2 e -3, o resultado será outro número inteiro, neste caso, -1.
Propriedade de fechamento sob subtração: A subtração de dois números inteiros sempre resulta em outro número inteiro. Por exemplo, se você subtrair dois números inteiros, como -4 e 5, o resultado será outro número inteiro, neste caso, 1.
Propriedade de fechamento sob multiplicação: A multiplicação de dois números inteiros sempre resulta em outro número inteiro. Por exemplo, se você multiplicar dois números inteiros, como -2 e 3, o resultado será outro número inteiro, neste caso, -6.
Propriedade de multiplicação com 1: Qualquer número inteiro multiplicado por 1 resulta no próprio número inteiro. Por exemplo, \(1 \times n = n\), onde \(n\) é qualquer número inteiro.
Propriedade de existência do oposto: Para cada número inteiro \(a\), há um único número inteiro \(-a\) (o oposto aditivo de \(a\)), de modo que \(a + (-a) = 0\).

Observe que os Inteiros possuem a propriedade de fechamento nas operações de soma, subtração e multiplicação mas não na divisão. Não há ainda uma forma de representar números decimais. Para fazer essa representação, foi criado o conjunto dos Números Racionais

Números Racionais

Os números racionais são todos os números que podem ser expressos como a razão (ou quociente) de dois números inteiros, onde o denominador não é zero. Em outras palavras, um número racional é qualquer número que pode ser escrito na forma de fração.

Formalmente, é definido como:
\( \mathbb{Q} = \left\{ x = \frac{a}{b} \middle| a, b \in \mathbb{Z}, b \neq 0 \right\} \), onde \( a \) e \( b \) são números inteiros e \( b \) não é zero.

Exemplos de números racionais incluem: \( \frac{1}{2} \) ,\( \frac{2}{1} \) ,\( \frac{3}{4} \) ,\( \frac{4}{3} \) ,\( -\frac{5}{6} \) ,\( -\frac{6}{5} \) ,2

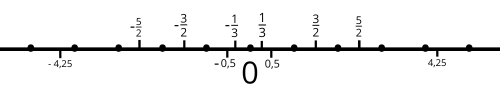
A reta numérica está preenchida com os racionais.

Propriedades dos Números Racionais

Propriedade de Densidade dos Números Racionais: Afirma que, dados dois números racionais \( a \) e \( b \), onde \( a < b \), sempre existe um número racional \( c \) tal que \( a < c < b \). Em outras palavras, entre quaisquer dois números racionais distintos, sempre há um número racional no meio.
Comparação entre dois Racionais: Os números racionais podem ser comparados entre si usando as operações de maior que (\(>\)), menor que (\(<\)), maior ou igual (\(\geq\)) e menor ou igual (\(\leq\)). Isso significa que podemos ordenar os números racionais em uma linha, do menor para o maior, ou vice-versa. Por exemplo, \( \frac{1}{2} < \frac{3}{4} \) e \( \frac{5}{6} > \frac{1}{3} \).
Todo número inteiro é um número racional: Cada número inteiro pode ser representado como uma fração com denominador 1. Portanto, todo número inteiro também é um número racional.
Propriedades de distributividade: As propriedades distributivas da multiplicação em relação à adição e subtração também se aplicam aos números racionais.
Existência de inversos multiplicativos: Todo número racional, exceto zero, possui um inverso multiplicativo. O inverso multiplicativo de um número racional \( \frac{a}{b} \) é \( \frac{b}{a} \), desde que \( a \) e \( b \) sejam diferentes de zero. A multiplicação de um número por seu inverso sempre é igual a 1.
Propriedades de identidade: Existem elementos identidade para adição (0) e multiplicação (1) nos números racionais, de modo que \( a + 0 = a \) e \( a \cdot 1 = a \) para qualquer número racional \( a \).
Propriedades de ordenação: Os números racionais podem ser comparados entre si usando as operações de maior que (\(>\)), menor que (\(<\)), maior ou igual (\(\geq\)) e menor ou igual (\(\leq\)). Isso significa que podemos ordenar os números racionais em uma linha, do menor para o maior, ou vice-versa. Por exemplo, \( \frac{1}{2} < \frac{3}{4} \) e \( \frac{5}{6} > \frac{1}{3} \).
Encadeamento de operações: Os números racionais possuem propriedades de fechamento sob adição, subtração, multiplicação e divisão. Isso significa que a soma, a diferença, o produto e o quociente de dois números racionais sempre resultam em outro número racional, desde que o divisor não seja zero.

Números Irracionais

Os números irracionais são números que não podem ser expressos como a razão de dois números inteiros. Em outras palavras, são números que não podem ser representados como frações simples. Os números irracionais são infinitos e não periódicos quando expressos na forma decimal.

Formalmente, o conjunto dos números irracionais é definido como \( \mathbb{I} = \mathbb{R} \setminus \mathbb{Q} \), onde \( \mathbb{R} \) é o conjunto dos números reais e \( \mathbb{Q} \) é o conjunto dos números racionais.

Exemplos de números irracionais incluem: \( \sqrt{2} \), \( \pi \), e, \( -\frac{\sqrt{2}}{5} \) ...

Propriedades dos Números Irracionais

Não podem ser expressos como frações simples: Os números irracionais não podem ser representados como frações simples, ou seja, não podem ser expressos na forma \( \frac{p}{q} \), onde \( p \) e \( q \) são números inteiros e \( q \neq 0 \).
Representação decimal infinita e não periódica: Quando representados na forma decimal, os números irracionais têm uma representação infinita e não periódica. Isso significa que seus dígitos decimais se estendem indefinidamente sem padrão repetitivo.
Existência em qualquer intervalo: Entre quaisquer dois números reais distintos, sempre há pelo menos um número irracional. Isso decorre da densidade dos números irracionais na reta numérica.
Conjunto denso na reta real: Os números irracionais são densos na reta real, o que significa que entre quaisquer dois números irracionais, sempre existe um número real racional ou irracional.
Não podem ser expressos como raízes exatas: Muitos números irracionais são representados como raízes quadradas de números inteiros. Por exemplo, \( \sqrt{2} \) é irracional porque não pode ser expresso como uma raiz exata de um número inteiro.

Números Reais

Os números reais compreendem todos os números que podem ser representados em uma reta numérica, incluindo números racionais e irracionais. Em outras palavras, os números reais abrangem todos os números, desde números naturais até números irracionais.

Formalmente, o conjunto dos números reais é denotado por:
\(\mathbb{R} = \{ x \in \mathbb{R} \mid x \in \mathbb{N} \cup \mathbb{Z} \cup \mathbb{Q} \cup \mathbb{I} \}\).

Propriedades dos Números Reais

Completude: Os números reais formam um conjunto completo, o que significa que não há "lacunas" na reta numérica. Em outras palavras, entre quaisquer dois números reais distintos, sempre existe outro número real.
Ordenação: Os números reais podem ser comparados entre si usando as operações de maior que (\(>\)), menor que (\(<\)), maior ou igual (\(\geq\)) e menor ou igual (\(\leq\)). Isso permite a ordenação dos números reais em uma reta numérica.
Operações Aritméticas: Os números reais possuem as propriedades das operações aritméticas, como adição, subtração, multiplicação e divisão. Essas operações obedecem às regras familiares de associatividade, comutatividade e distributividade.
Propriedades de Fechamento: As operações aritméticas entre números reais resultam em números reais. Por exemplo, a soma, a diferença, o produto e o quociente de dois números reais sempre produzem outro número real, desde que a divisão não seja por zero.
Densidade: Os números reais são densos na reta real, o que significa que entre quaisquer dois números reais distintos, sempre existe um número real. Isso decorre da infinitude dos números reais e da sua capacidade de preencher todos os intervalos na reta numérica.
Existência de raízes: Todo número real não negativo possui uma raiz quadrada real não negativa. Além disso, todo número real possui uma raiz n-ésima real. Essas propriedades garantem que as operações de radiciação sejam definidas para todos os números reais.